Kolmogorov-Arnold Networks
数学机理
基于Universal Approximation Theorem(UAT)的Multilayer Perceptron(MLP)作为构建神经网络的基本组件,由于其可以拟合任意函数的能力其本身及其变体在过去几十年来被广泛使用。然而由于其不可解释性,长期以来饱受诟病。近日,一个基于Kolmogorov-Arnold Representation Theorem(KART)的新神经网络结构Kolmogorov-Arnold Network(KAN)[5]被提出,在各项指标中都有替代MLP之势。本文对这个新结构KAN进行简单解读。
首先重述一下MLP的原理,ML本质上是寻找/拟合一个尽可能逼近一个需要但不一定完全正确的函数。那么为什么MLP如此naïve的结构可以拟合我们可能想寻找的万千函数?UAT告诉我们,在包含足够多隐层神经元的FNN可以以任意精度近似任何连续函数。也即是,无论我们的目标函数有多复杂,一定存在一个NN可以以任意高的精度去近似,进一步地,也即是NN理论上可以解决任何近似问题,这也是近年PINN在求解ODE/PDE上大放异彩的原因。
Theorem 1(Universal Approximation Theorem[1]). $\forall n,m \in \mathbb{N}, \varepsilon > 0$,闭区间$K \subseteq \mathbb{R}^n$及其上的连续函数$f: K \mapsto \mathbb{R}^m$,存在$k\in \mathbb{N}, W\in \mathbb{R}^{k\times n}, b\in \mathbb{R}^{k}, C\in \mathbb{R}^{m\times k}$,使得:
\begin{equation}
\sup_{x\in K}|f(x)-C\cdot(\sigma\circ(W\cdot x+b))| < \varepsilon.
\end{equation}
其中$\sigma:\mathbb{R}\mapsto\mathbb{R}$为激活函数。
但是遗憾的是,这个定理是一个存在性定理,定理本身没有给出如何构造的指导,关于如何更好逼近的大量工作都是经验性的。同时在很多结构中,例如Transformer,MLP的参数量异常巨大,这给NN的可解释性问题更加蒙上了一层阴影。为此,业界一直在寻找MLP的一种替代性方案,目标是使用更少的参数获得同等或者更好的效果,并且具有较强的可解释性。
早在1993年,就有研究发现KART在多层感知器的研究中扮演着类似于通用逼近定理的角色[2],本文的工作也启发自KART。Theorem 2即是KART的表述。
Theorem 2(Kolmogorov-Arnold Representation Theorem[3]). 如果$f$是多元连续函数,则$f$可以写成单变量连续函数与二元加法运算的有限复合。也即是:
\begin{equation}
f(\mathbf {x} )=f(x_{1},\ldots ,x_{n})=\sum _{q=0}^{2n+1}\Phi _{q}\left(\sum _{p=1}^{n}\phi _{q,p}(x_{p})\right).
\end{equation}
其中:$\phi_{q,p}: [0,1]\to \mathbb{R}, \Phi_{q}: \mathbb{R} \to \mathbb{R}$。
这个定理还给出了一个重要的陈述:多元函数的本质就是加法,因为均可以由一元函数和加法构造出来[4]。这里再给出一个$n=2$的示例,如图1所示。
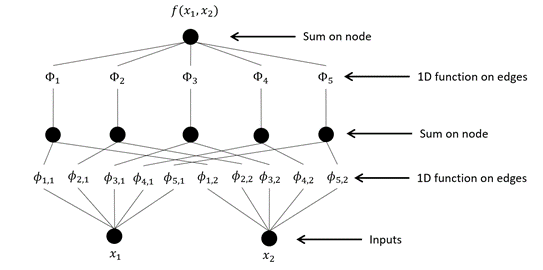
注意到无论是外层函数$\Phi$还是内层函数$\phi$这里都是一元函数,一个直观的理解就是可以直接用图像表示出来,如图2所示。
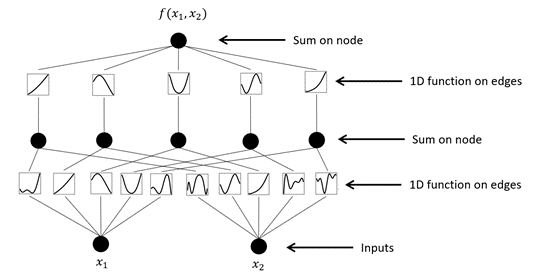
KAN的结构
注意到KART的表示可以立马转换为一个网络,这早在上世纪九十年代就有人意识到了,当时叫Kolmogorov Network特指这个两层的单输出结构,如图3所示。那么自然的,这结构可以类似于MLP的抽象,并且定义为KAN Layer。并且可以把网络做得更深。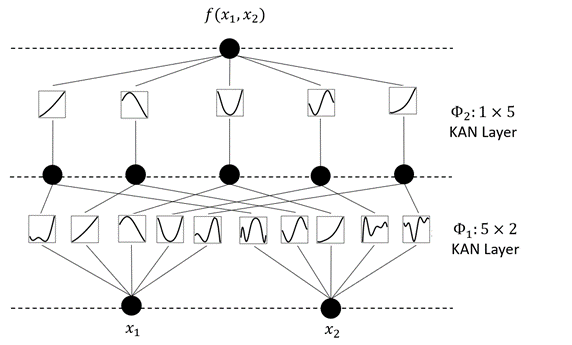
KART明确两层结构就可以完成拟合任务,那么为什么我们需要研究更深的KAN结构呢?实际上KART没有约束函数ϕ的数学性质,有可能是病态甚至是分形的。我们更希望使用光滑可导的函数来表达目标,以期能使用更方便的优化方式。
举个例子,$e^{\sin(x_1^2+x_2^2)+\sin(x_3^2+x_4^2)}$这个结构确实需要三层的结构去拟合。如动图4所示就是其训练的过程,我们发现如果是一层3层的KAN,那么在训练结束后确实可以在每一层得到和理论结果对应的激活函数。
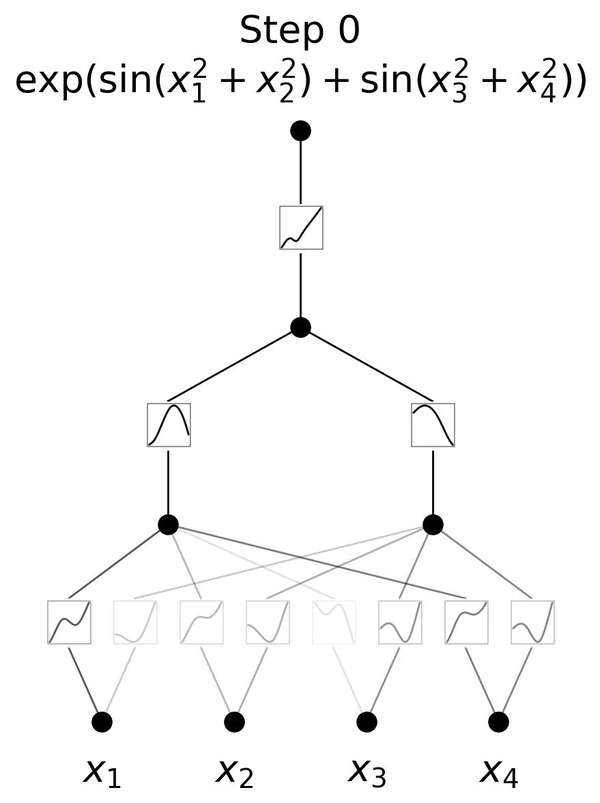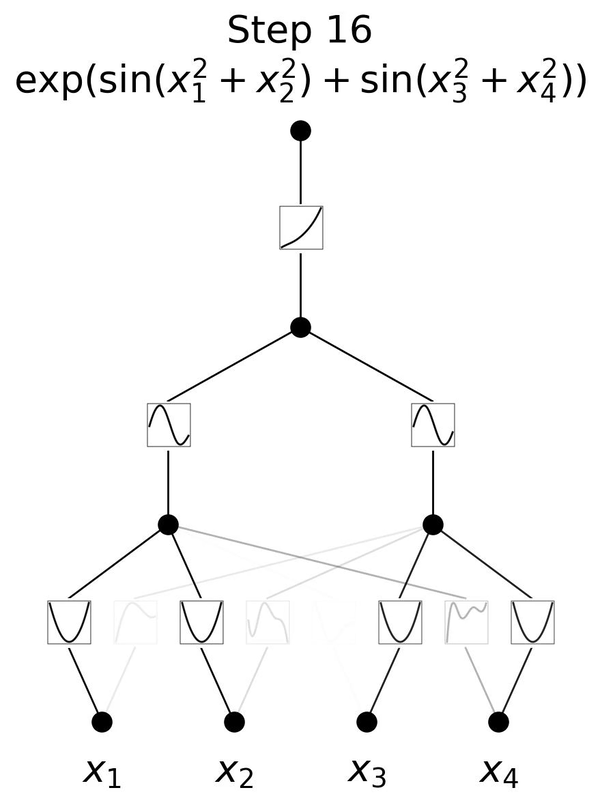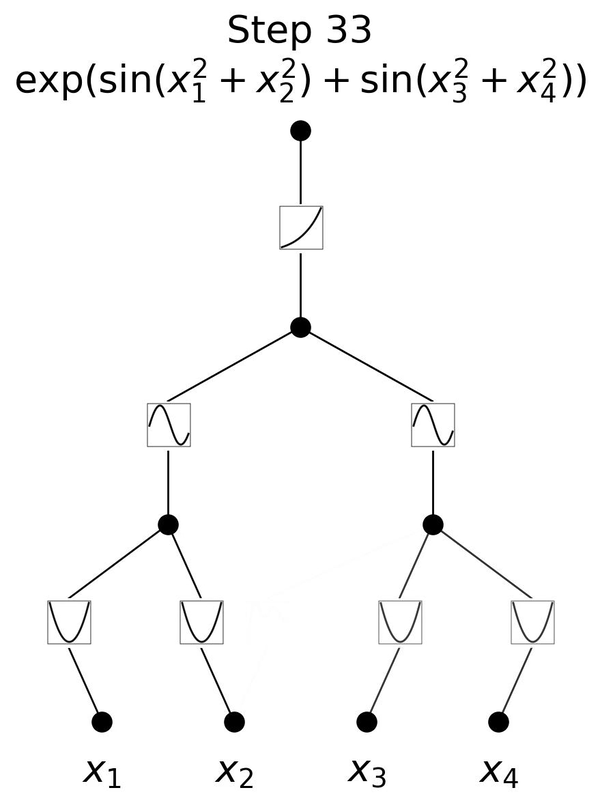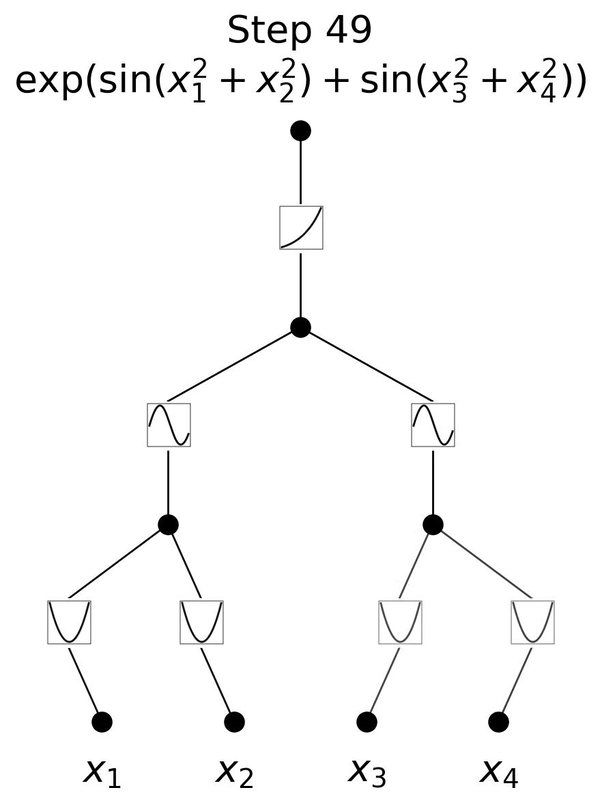
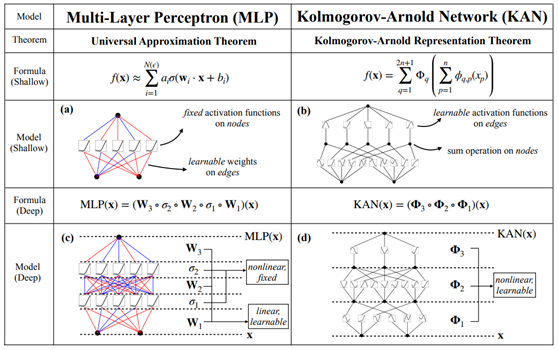
如图5所示,展示了MLP和KAN的一些对比。值得一提的是,MLP和KAN背后的表示论基础,也即是UAT和KART,这二者之间的联系还相当不清楚,这二者孰优孰劣也没有定论。就模型结构而言,二者一个主要差别是MLP的激活函数在模型节点上,而KAN是在边上。
算法细节
本节将简单描述一下KAN在实现过程中的一些算法细节,虽然原论文中的理论做了一些理论上的证明以期保证了其收敛,但其实算法本身非常简单几句话就能说明白,这也是这个工作较为难能可贵的地方。
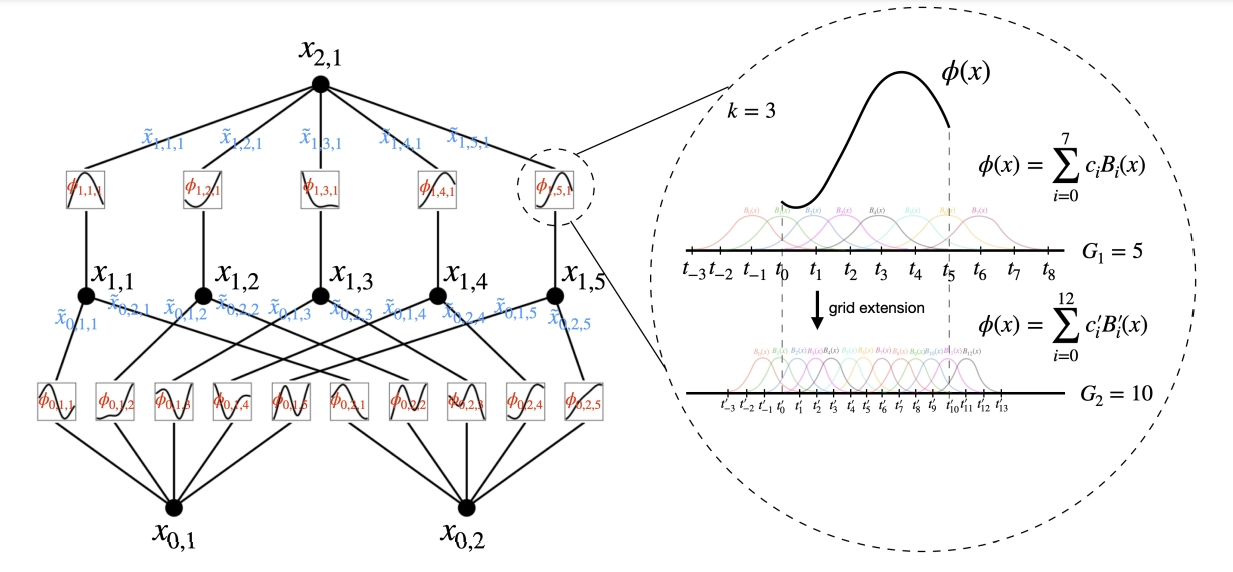
第一个问题是,如何把上面所说的一元函数转化为或者参数化为一个可学习的激活函数。那么本质上就是构造一种一元函数,样条函数应该是一个不错的选择。简单来说,样条函数就是一种分段函数,在每一段都具有连续的导数,最后。在论文中使用了B样条,如图6所示,B样条可以设置一些样条基函数,最后这个样条函数就是这些基函数的线性组合。所以真正学习的参数就是这个线性组合的系数$c_i$。样条函数一般在低维空间的函数逼近任务上效果很好,因此这个选择可以说是很自然的,同时注意到基函数具有连续导数,那么整个网络就是可导的,也即可以使用BP来训练。而B样条的基函数可以使用Cox-de Boor递归公式来定义,这个公式很优雅,但是涉及到递归求解,所以这一步是比较耗时的。样条函数还有个好处就是,我们可以在不同的分段细粒度上面切换,如图6所示,$G_1=5$和$G_2=10$分别就是一个比较粗和比较细的网格划分,这个好处就是在网络结构正确的情况下,如果我们有更多的数据,我们不需要重新训练网络,只需要把网格划分变细,就能简单地得到一个更好的网络。
在原始的实现中,作者使用了一些技巧,与其是技巧,不如说是实际上是作者尝试的很多方法中,他试出来第一个能work的结果。作者承认在这一部分还有更多的优化空间。第一个trick是Residual activation functions,如果我们一开始就直接把激活函数设置为样条,那大概率这是一些局部光滑但全局不那么光滑的函数,它对于loss landscape是不好的。因此作者在样条函数之上添加了一个光滑的基座作为初始化,这里选用了SiLU函数。样条的系数初始化几乎为0,这个和残差链接有一点相似。第二个是激活范围的问题,这个在MLP当中也存在,一般希望节点激活输出后,激活值尽可能保持在区间$[0,1]$之间,这里选用的方案是把基函数系数$c_i\sim\mathcal{N}(0,\sigma^2)$,方差$\sigma$是一个较小的数。在整体外设置权重$w$来控制整体激活函数的幅值,并且和MLP同样使用Xavier初始化。最后一点是,由于样条函数的定义域是有界的,而每一层的输出并不确定,所以自然需要动态地更新这个网格区间,作者经过了相当多的尝试后,采用了每训练迭代20次,对节点输出的范围做一次估计,根据其分布再来重新划定区间。
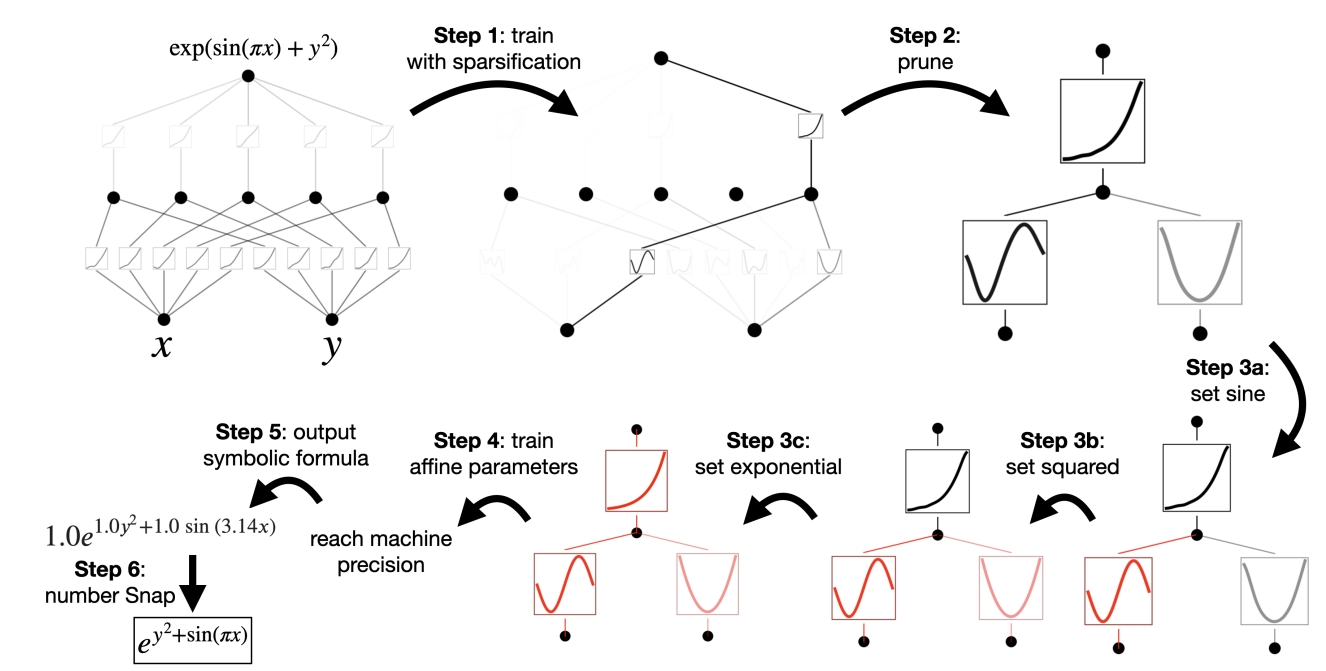
把细节讲明白之后最后我们完整地讲讲其训练过程。首先从一个全连接的KAN开始,第一步是通过一个修改过的L1正则把网络变得更稀疏,把较小权重的链接剪枝;有意思的地方来了,由于一元函数的图像人类是比较熟悉的,这时候根据观察一元函数的图像以及其具体值,人类是可以猜测这个一元函数的的符号形式,如图7所示,猜测这个结果是正弦、平方和指数函数,全部设置完毕后,求解出来的结果是可以达到机器精度的。这样是可以求解出正切的符号公式的,这个决策过程相当透明化,也具有很强的可信度和可解释性。虽然这个学习也可以全自动化不需要人类干预,但是实际上在很多任务下,就是需要人类先验知识才能获得更好的效果。
性质和效果
上面我们讲了KAN是什么,接下来我们来介绍KAN有上面好处,更中性的说法是首先尽量理解其性质再说它的好处。
首先我们注意到的是这个Scaling性质,这个在摩尔定律和LLM中有很多体现。简而言之就是模型的参数量越多其表现越好。不严谨地讲,具体到公式(Neural scaling laws)上就是$\ell\propto N^{-\alpha}$,其中$\ell$是近似误差(Loss/Error),$N$是参数量,$\alpha$是缩放比例指数(scaling exponent)[6]。就$d$元的样条函数而言,$\alpha=(k+1)/d$,其中$k$是基函数的阶。而根据KART,这里的$d=1$。很显然,这是一个比较理想的界,比MLP的理论上界要好很多。
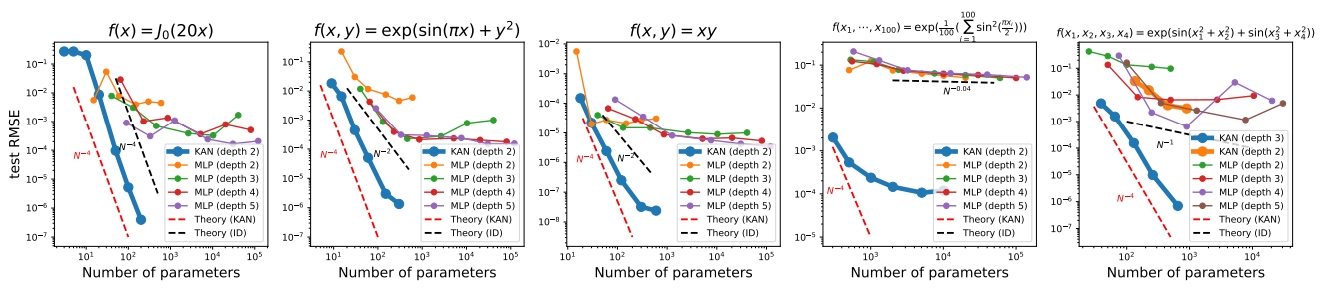
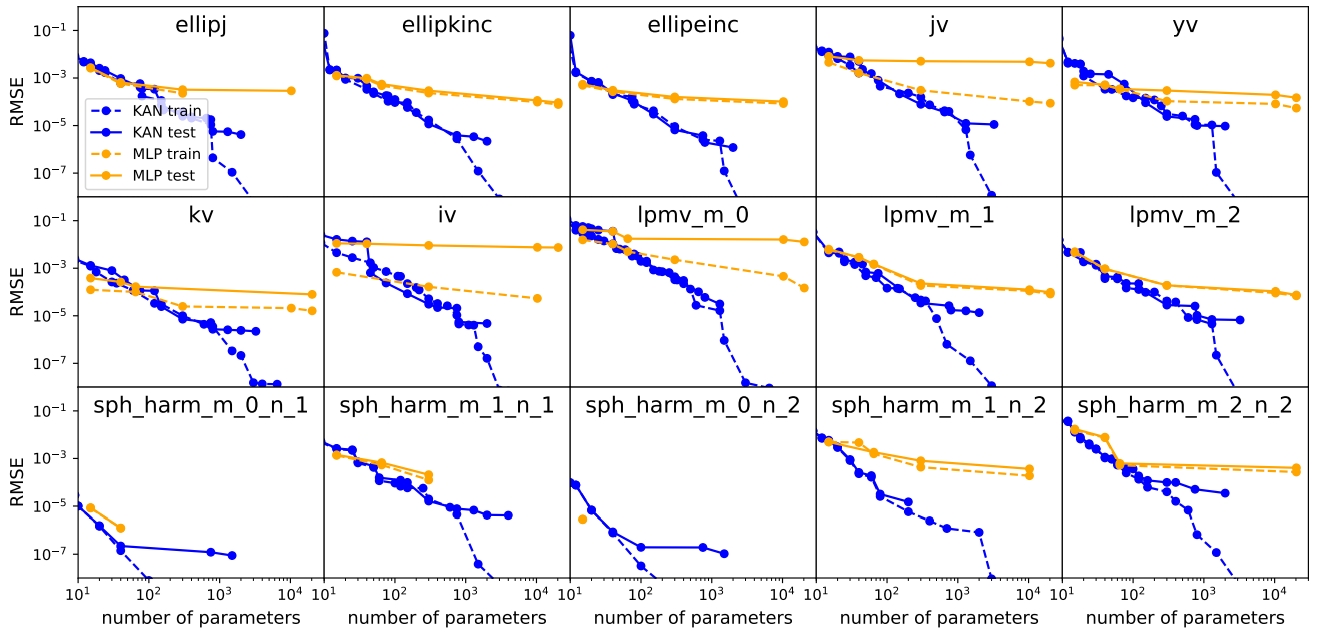
正是因为 KAN 的收敛速度比 MLP 更快,因此具有较少参数的KAN比MLP 可以获得更加的准确性的准确性,如图8所示。即便是特殊函数,如图9所示,我们用模型参数的数量和RMSE损失在平面上展示了KAN和MLP的Pareto Frontiers 。在所有特殊函数中,KAN都比MLP具有更好的Pareto Frontiers(关于Pareto Frontiers的概念请参考[7])。
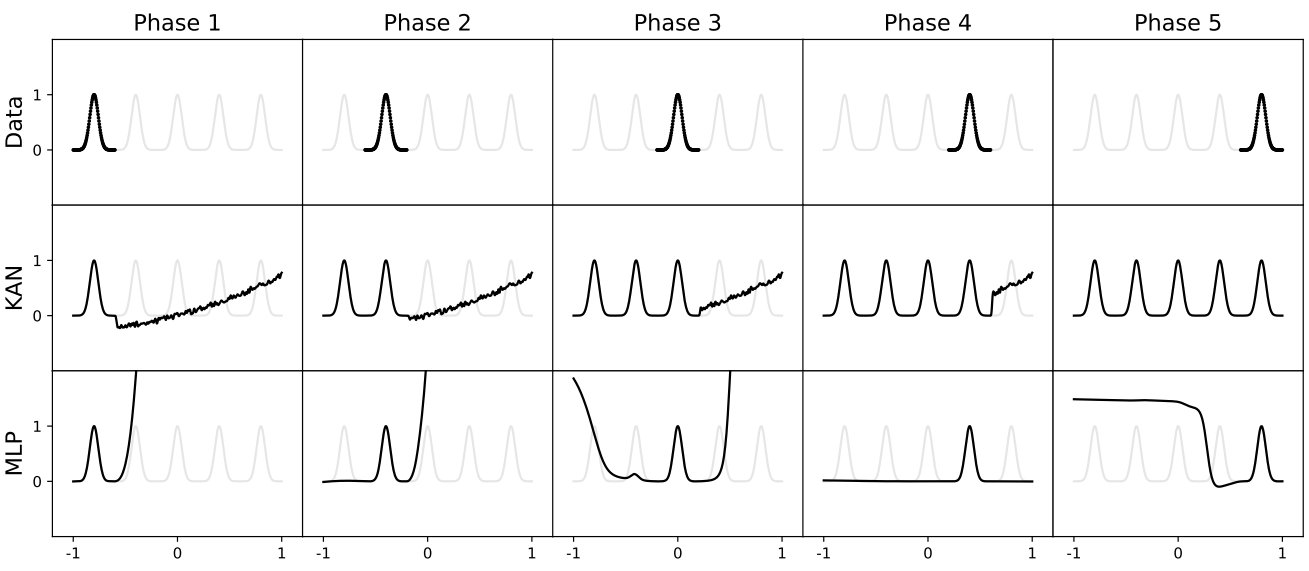
灾难性遗忘几乎是困扰所有机器任务的问题,而KAN由于其结构具有局部可塑性,可以通过利用样条的局域性来避免灾难性遗忘。这是因为样条基函数是局部的,一个样本只会影响附近的几个样条系数,而留下较远的系数不变(这是可取的,因为较远的区域可能已经存储了我们想要保存的信息)。相比之下,由于MLP通常使用全局激活,例如,ReLU/Tanh/SiLU等,任何局部变化都可能不受控制地传播到遥远的区域,破坏存储在那里的信息。如图10所示,展示了一个简单的持续学习问题。数据集是一个具有5个高斯峰的1D回归任务(最上面一行)。每个峰值周围的数据按顺序呈现(而不是一次全部呈现)给KAN和MLP。KAN(中排)可以完全避免灾难性遗忘,而MLP(下排)则表现出严重的灾难性遗忘。
应用与批评
由于KAN的开创性和对MLP的直接可替代性,在预印本论文发布以来,极短时间内有大量的同行对其进行了大量的改进和实验,在业内有较为重大的影响。截至目前已经有一些工作得到了同行的认可,这里我们做一个简单的介绍。
针对于KAN的原本实现计算缓慢的问题, EfficientKAN将计算重新表述为用不同的基函数激活输入,然后将它们线性组合。这种重新表述可以显著降低内存成本,并使计算成为简单的矩阵乘法,并且可以自然地处理向前传递和向后传递。显著提升了其计算效率。同时,不同结构的神经网络也尝试将原来的连接方式变为了KAN链接,例如 GraphKAN和 ConvolutionKAN,也获得了一些效果。同时在大语言模型上,KAN-GPT和 Kansformer相继进行了实验,基本可以做到快速精度提升的效果。KAN作为一个即插即用的模块,基本可以无差别的对现有MLP结构做直接替换。
虽然KAN在的讨论程度极高,但是其效果还没有经过大规模验证和同行评议。而美国科学院院士, PINN(Physics-Informed Neural Network)发明者,布朗大学George Karniadakis教授在社交网络上公开质疑KAN的效果,原论文声称KAN在求解ODE/PDE有很好的效果,但是George院士表示使用了KAN作者在GitHub上的代码给对求解NS方程出了完全错误的结果,甚至对最简单的泊松方程的求解都得到了24%的误差。此外,论文对于光滑样条后的存在性证明也没有良好的叙述,什么样的目标函数能够使用KAN进行表述这在数学上没有保证或者限制,边界条件没有做任何讨论。目前做PDE/ODE的科学家对该方法的有效性大规模存疑。
Reference
[1]: Funahashi K I. On the approximate realization of continuous mappings by neural networks[J]. Neural networks, 1989, 2(3): 183-192.
[2]: Lin J N, Unbehauen R. On the realization of a Kolmogorov network[J]. Neural Computation, 1993, 5(1): 18-20.
[3]: Arnold H K. Dessert: Hilbert’s 13th Problem, in Full Colour[J].
[4]: Diaconis P, Shahshahani M. On nonlinear functions of linear combinations[J]. SIAM Journal on Scientific and Statistical Computing, 1984, 5(1): 175-191.
[5]: Liu Z, Wang Y, Vaidya S, et al. Kan: Kolmogorov-arnold networks[J]. arXiv preprint arXiv:2404.19756, 2024.
[6]: Hestness J, Narang S, Ardalani N, et al. Deep learning scaling is predictable, empirically[J]. arXiv preprint arXiv:1712.00409, 2017.
[7]: Goodarzi E, Ziaei M, Hosseinipour E Z. Introduction to optimization analysis in hydrosystem engineering[M]. New York, NY, USA: Springer International Publishing, 2014.